Temporal scales and signal modeling in dendroclimatology

Guiot J

>Access contents of this issue

>Download this article as pdf

Past Global Changes Magazine

25(3)

142-143

2017

https://doi.org/10.22498/pages.25.3.142

Joël Guiot

Tree rings are demonstrably good proxies for temperature or precipitation at timescales less than a century. Reconstruction based on multiple proxies and process-based modeling approaches are needed to estimate the climate signal at lower frequencies.

Paleoclimatological proxies "represent records of climate that were generated through physical, chemical and/or biological processes. Reconstructions of climate rest on attempts to turn this around in order to get back to the climate information" (Hughes et al. 2010). In most cases these reconstructions are obtained as chronological series, which are characterized by a time resolution depending on the sedimentation or growth processes. These processes act as a low-pass filter and determine the resolution of the climatic signal. Here, I focus specifically on tree-ring series.

Pre-processing of tree-ring series

Tree-ring series reproduce annual variability of the climate with relatively good reliability, but tree growth is the result of numerous complex processes. Hence, like all biological proxies, tree rings record a combination of several climate variables. At low frequencies, the signal is affected by an age-related trend, which includes both geometrical and physiological factors. During its young phase, the tree builds its architectural model and leaf system, and then reaches its reproductive maturity with a progressive increase of biomass production. This is the physiological component of the trend. Afterwards, the tree leaf area stabilizes, and a fairly constant quantity of xylem is distributed along a circle of increasing diameter. This is the geometry factor. Other low-frequency effects may occur during the tree’s lifespan, such as competition variations, changes in nutriment availability and carbon concentration in the atmosphere, fires, infestations, diseases, or genetic variability – and climate changes. All these factors result in a complex combination of low and mid frequency signals, which should be understood and modeled to produce indices for climate reconstructions.

The classical approach, called the standardization, consists of detrending tree-ring time series before calibration with meteorological time series. Numerous methods exist, but it is difficult to distinguish the low-frequency signals related to climate from other factors (Cook and Kairiukstis 1990). The standardization produces indices, which are defined as the ratio between the raw tree ring and a theoretical model of (low-frequency) growth, either calculated by nonlinear functions, smoothing, autoregressive models or a function based on the biological age of the tree (Briffa and Melvin 2011). The latter method is complex and needs a large number of replicated series for the same species. No method is perfect and some of them reduce the low-frequency signal excessively, while others introduce spurious low-frequency variations. For these reasons, climate reconstructions tend to be biased, with either too little or too much low-frequency variability.

Climate reconstructions

Climate reconstruction consists of calculating a regression between climate series and tree-ring series on the period where both are available (usually the last century) and to extrapolate the regression, also called transfer function, to tree-ring series of previous centuries. These reconstructions may be affected by the so-called "divergence problem". From the 1970s, the tree-ring series no longer appears to be correlated with summer temperature, especially in the high latitudes and in some cases in the high elevations (D’Arrigo et al. 2008). The correlation shifts towards the summer precipitation or other climate factors. The shift may be caused by a change of limiting factors (climate becoming warmer, trees are lacking water), an effect of CO₂ fertilization, air pollution, soil composition change (increase of nitrate), or insolation. This induces a calibration bias: if the transfer function is calibrated on the most recent period (after the 1970s), it should not be used to estimate climate variations before the 1970s. This problem triggered some worries about the value of the climate reconstructions.

Despite these risks of biases, and likely because of them, numerous statistical reconstruction methods have been introduced after the pioneer paper to deconvolve the climatic signal (Fritts et al. 1971). Tree rings are indeed an interesting material for statisticians because the time series have annual resolution and they are also well replicated (a site tree-ring series is based on 20 to 50 cores).

The climate signal calibration is often based on multiple regression, but the low-frequency signal may differ depending on the stationarity of the time series, on the calibration period, the use, or not, of the principal components, the rescaling done after the calibration and other variations (Bürger et al. 2006). Pseudo-proxy method is an interesting method to study the behavior of the reconstruction method. It consists (i) in generating proxy series from climate model simulation to which are added white noises of progressively increased variance, (ii) in calibrating the reconstruction method on the pseudo proxy series, and (iii) analyzing the performance of the method in function of the noise variance. A difficulty is that these pseudo-proxies should mimic as best as possible the physics of the proxies used (Christiansen and Ljungqvist 2016).

Other variables may be measured on tree rings and used for estimating past climates. They have not the same biases but can have others. The tree-ring maximum density has proved to be quite useful to reconstruct the summer temperature and seems to be free of age-related trends (Briffa et al. 1992). Oxygen isotopes (δ¹⁸O) in cellulose is a potential means to reconstruct variables related to water (Saurer et al. 1997). Stable carbon isotopes (δ¹³C) record the balance between stomatal conductance and photosynthetic rate, dominated at dry sites by relative humidity and soil water status, and at moist sites by summer irradiance and temperature (McCarroll and Loader 2004).

Moberg et al. (2005) proposed to use both pollen data and tree rings to reconstruct Northern Hemisphere average temperature. Pollen data are robust on low frequencies, so that they could help improve the quality of the low-frequency part of the signal. This application used a wavelet analysis. A similar approach has been used by Guiot et al. (2010) for gridded temperature in Europe, using a method of spectral decomposition. A calibration is done separately in the low-, medium- and high-frequency bands with the appropriate proxies.

Process-based approaches

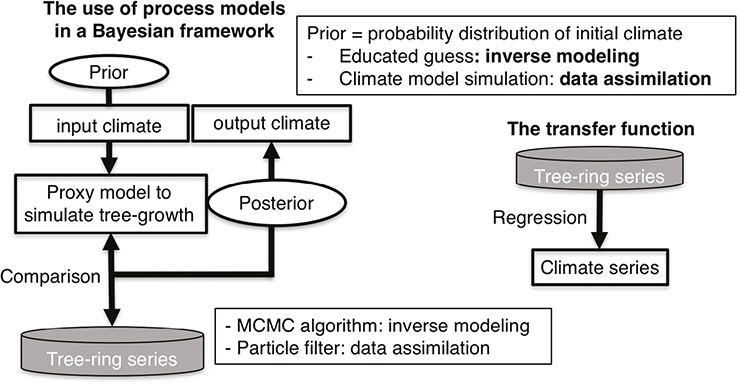
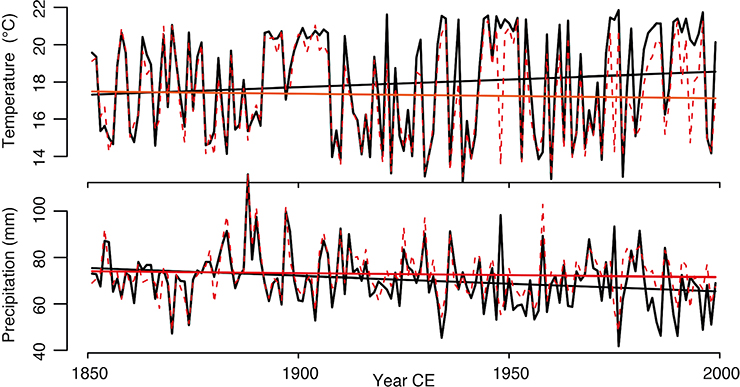
Figure 1: Diagram of the process-based approach and comparison with the standard transfer function. In the process-based approach, the initial probability distribution of the climate (needed to initiate the iterations) may be given by educated guess, as it is done with the class of methods called inverse modeling, or by simulation of climate models, as it is done with the class of data assimilation methods. The standard transfer function uses the tree-ring series as input and the climate as output. The stream is opposite to the causal relationships.

Finally, one may model the formation of the record by representing explicitly the chain of physical and biological processes which lie between the climatic information and the observed signal. Such a model may be used in "forward mode", forced by climatic or other environmental data (Fig. 1). It may also be inverted to estimate climate from observations, as in the MAIDEN or VS-light models (Boucher et al. 2014; Tolwinski-Ward et al. 2014). The inverse problem is solved with a Bayesian method, which estimates the posterior probabilistic distribution of the climate parameters providing the observed tree growth. When the processes generating the low-frequency discrepancies are included in the model, it is possible to clear the climate reconstruction from the corresponding biases, such as the CO₂ effect. This process is illustrated in Figure 2. Scenario A1 (black) forces the inversion with true values of CO₂ concentration while scenario A2 (red) forces the inversion with constant CO₂ concentration (280 ppmv). Both reconstructions are highly correlated in the high-frequency domain. When the CO₂ effect is not taken into account (A2), the temperature reconstruction has no linear trend (the differences are not significant for the precipitation). As this temperature trend is also recorded in the observations (not shown here), it is important to take into account the CO₂ effect to obtain better reconstructions in the low-frequency domain. Another approach based also on process models, which seems also promising, is data assimilation, in which proxy data are used in conjunction with model runs (Acevedo et al. 2016; see also Fig. 1).

Conclusion

Figure 2: Summer temperature and precipitation reconstructions at Fontainebleau, France, obtained from the inversion of the multiproxy biophysical model MAIDENiso (Boucher et al. 2014), i.e. the MAIDEN model with an isotope simulation module. Red curves are obtained when the inversion is forced by CO₂ fixed at preindustrial levels (280 ppmv) and black curves are obtained from increasing values of CO₂ from 280 ppmv in 1850, 320 ppmv in 1960 to 360 ppmv in 2000. Straight lines with corresponding colors represent the trends. Adapted from Boucher et al. (2014).

In conclusion, tree-ring series have an excellent time control and an annual resolution, and are good proxies for temperature or precipitation variations (depending on their geographical position and species) at sub-century timescales. At lower frequencies, literature is extensive on the difficulties coming from (i) the standardization procedure (age-related factors), (ii) the selection of model relating tree growth and climate, and (iii) the calibration of the model itself. Proposed solutions are based on multiproxy approaches, use of appropriate treatment of low frequencies, and, finally, mechanistic tree-growth models.

affiliation

CEREGE, CNRS, Aix-en-Provence, France

contact

Joël Guiot: guiot@cerege.fr

references

Acevedo W et al. (2016) Clim Dyn 46: 1909-1920

Boucher E et al. (2014) Biogeosciences 11: 2014-3245

Briffa K, Melvin T (2011) Dendroclimatology 5: 1-30

Briffa KR et al. (1992) J Clim 5: 735-753

Bürger G et al. (2006) Tellus A 58A: 227-235

Christiansen B, Ljungqvist FC (2016) Rev Geophys 55: 40-96

Cook ER, Kairiukstis LA (1990) Methods of dendrochronology. Applications in the environmental sciences. Kluwer Academic Publishers, 393pp