- Home
- Publications
- PAGES Magazine
- Advances In Glacial Isostatic Adjustment Modeling
Advances in glacial isostatic adjustment modeling
Milne GA, Al-Attar D, Whitehouse PL, Crawford O & Love R
Past Global Changes Magazine
27(1)
16-17
2019
Glenn A. Milne1, D. Al-Attar2, P.L. Whitehouse3, O. Crawford2 and R. Love4
We overview two PALSEA-relevant applications of glacial isostatic adjustment modeling and highlight recent advances. These include the consideration of models with lateral Earth structure and the development of methods to determine optimal parameters and model uncertainty.
The primary aim of the PALSEA (PALeo constraints on SEA level rise) working group is to promote and improve the use of constraints from observations and modeling of past sea-level changes and ice-sheet extent to better inform projections of future sea-level change. Glacial isostatic adjustment (GIA) – the deformational, gravitational and rotational response of the Earth to past ice-sheet evolution – plays an important role in reaching this objective in several respects (see Editorial, this issue). Here we review recent advances in two key PALSEA-relevant GIA model applications - estimating global ice volume during past warm periods and the contribution of GIA to future sea-level change - and consider recent developments towards improving uncertainty estimation in GIA model output which is central to these applications.
Estimating global ice volume during past warm periods
A core aim of PALSEA is to estimate the peak in global mean sea level (GMSL), from which global ice volume can be inferred, during past warm periods when GMSL was greater than at present. There are three periods in relatively recent Earth history for which observations indicate that GMSL was above the present value: the Mid-Pliocene warm period (~3 Myr BP), Marine Isotope Stage 11 (~420-370 kyr BP), and Marine Isotope Stage 5e (~129-116 kyr BP; the Last Interglacial). Estimating GMSL from a sparse distribution of local relative sea level (RSL) indicators is non-trivial due to under-sampling and the fact that local sea level can depart significantly from the global mean value. GIA is one of a number of processes (e.g. dynamic topography and sediment loading; see contributions on these topics in this issue) that should be considered when estimating GMSL from RSL records. A small number of studies have demonstrated that the GIA “overprint” can significantly bias estimates of GMSL for each of the three warm periods mentioned above (e.g. Raymo et al. 2011; Raymo and Mitrovica 2012; Kopp et al. 2009; Dutton and Lambeck 2012; Dendy et al. 2017). Specifically, they show that the GIA contribution to RSL can range from order 1-10 m depending on the data location and the choice of model inputs (parameters).
Regarding model inputs, the ice-loading history and Earth viscosity structure are the most important. There is considerable uncertainty in both of these, so it is necessary to perform model-sensitivity analyses to map out which parametric uncertainty dominates at the specific data locations. The analysis of Dendy et al. (2017) is the most thorough in this respect. In addition to uncertainty in model parameters, limitations in the model itself, due to, for example, missing processes or simplifications in the geometry, can lead to considerable error or bias in the output (formally known as model structural error). A recent advancement in this area is the development of coupled models that account for feedbacks between GIA-related processes and ice dynamics (see Whitehouse 2018). One limitation in all of the GIA studies noted above is the use of spherically symmetric Earth models in which parameters vary only with depth. GIA models that include a 3D Earth structure have been applied in some studies that consider post-Last Glacial Maximum sea levels or geodetic observations (Whitehouse 2018) and the impact has been shown to be non-negligible. However, the computational expense of these models currently prohibits their use for earlier times such as those mentioned above due to the longer time integrations required.
The contribution of GIA to future sea-level change
The construction of comprehensive regional RSL projections, which requires the compilation and summation of contributions from different processes, has only been attempted relatively recently (e.g. Slangen et al. 2014). In regions that were recently deglaciated, GIA will be a significant contributor to future RSL change. The GIA component has been either explicitly included using process model output (Slangen et al. 2014) or estimated from tide-gauge records as part of a linear trend that could also include other secular processes (for example, tectonics; Kopp et al. 2014). In the former case, one issue has been the lack of accurate uncertainty estimates on GIA model output.
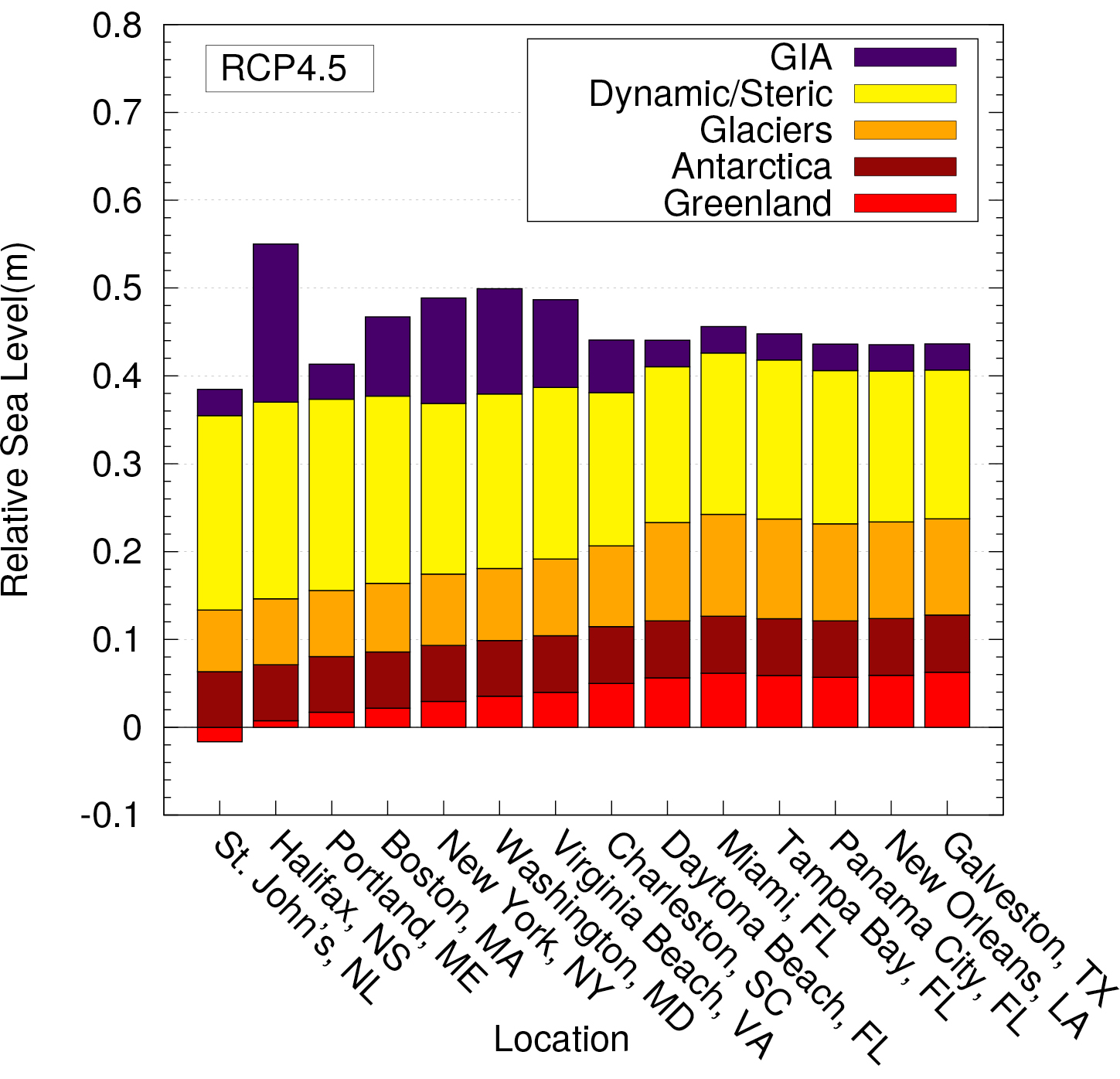
Recent studies (Love et al. 2016; Yousefi et al. 2018) have sought to address this issue by using a large suite of model runs sampling a broad range of Earth and ice-model parameters as well as a state-of-the-art regional RSL database to estimate model uncertainty. The PALSEA-led effort to produce regional RSL databases using standard protocols (Khan et al. this issue) has greatly enhanced the quality and availability of these databases, facilitating improved GIA model development. The studies of Love et al. (2016) and Yousefi et al. (2018) demonstrate the relative importance of GIA for future sea-level change along the Atlantic and Pacific coasts of North America (e.g. Fig. 1) and, perhaps more importantly, that uncertainty in defining the GIA contribution is large and that spherically symmetric Earth models are not able to accurately reproduce observations of recent RSL change in these regions.
Towards improved GIA models
Two key aspects of GIA model development relevant to the applications outlined above include the use of Earth models that can accommodate lateral Earth structure as well as methods to estimate model parameters and the uncertainty associated with each. Past studies have used large ensemble forward modeling and statistical methods to estimate uncertainty in the ice (e.g. Tarasov et al. 2012) and spherically symmetric Earth models (e.g. Caron et al. 2017). Given the interdependence of these model inputs, future analyses should aim to jointly infer ice- and Earth-model parameters and their uncertainty. Estimating parametric uncertainty is more challenging with 3D Earth models given the much larger parameter space and the uncertainty in constraining lateral viscosity structure (Whitehouse 2018).
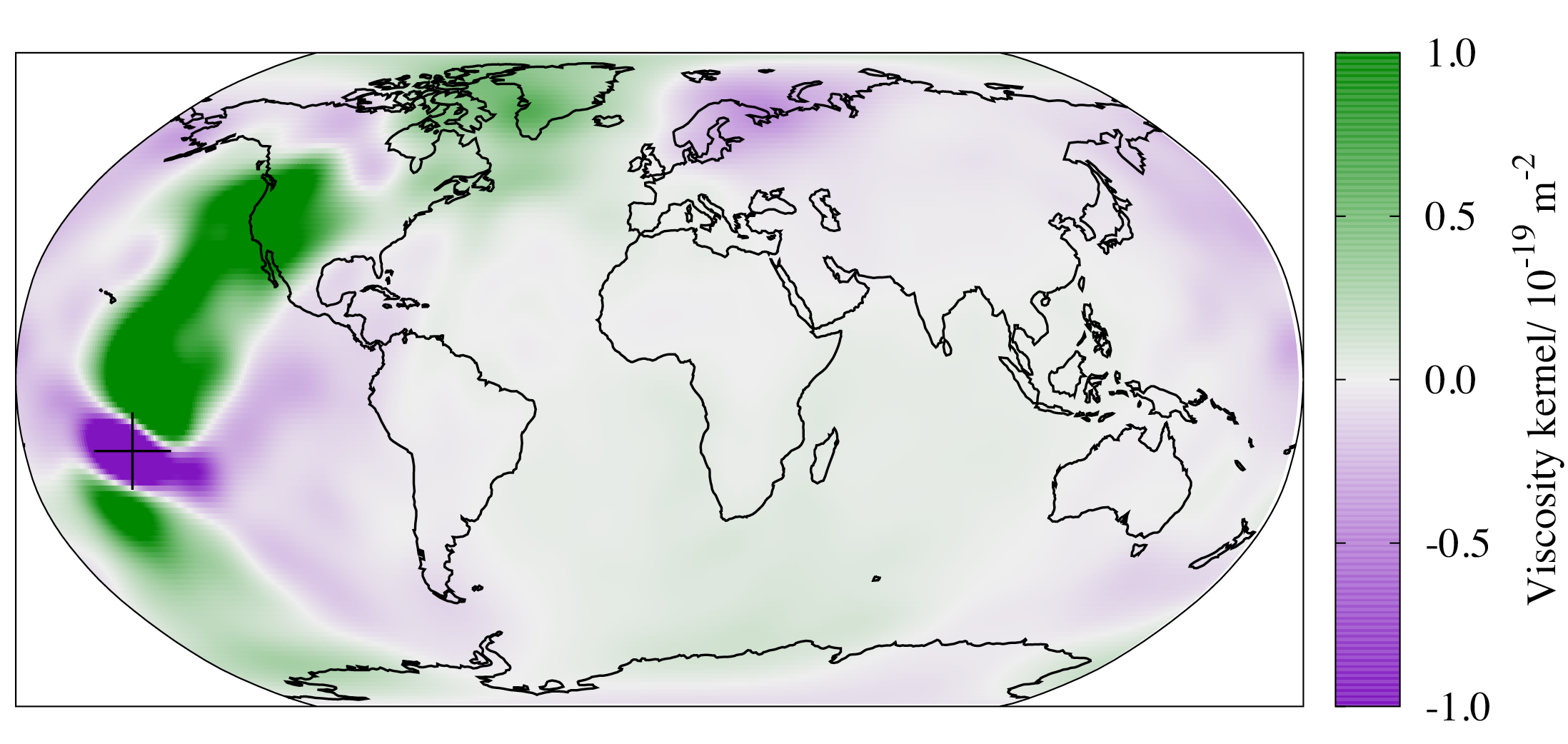
A step towards overcoming the latter issue is the determination of sensitivity kernels for GIA observables. These kernels quantify the linearized dependence of observations on underlying parameters, and can be used in both inversions and uncertainty quantification (Fig. 2). Early studies estimated such kernels using finite-difference approximations (e.g. Zhong et al. 2003), but here the computational cost scales with the number of model parameters, and so rapidly becomes infeasible. A better approach is through the use of the adjoint method, which produces exact kernels at the cost of just two forward simulations (Al-Attar & Tromp 2014). Using this approach, the inversions for ice history and 3D Earth structure from GIA observables is a realistic goal, with promising synthetic tests having been performed recently (Crawford et al. 2018; Fig. 2).
affiliations
1Department of Earth and Environmental Sciences, University of Ottawa, Canada
2Department of Earth Sciences, University of Cambridge, UK
3Department of Geography, Durham University, UK
4Department of Physics and Physical Oceanography, Memorial University of Newfoundland, St John’s, Canada
contact
Glenn A. Milne: gamilne@uottawa.ca
references
Al-Attar D, Tromp J (2014) Geophys J Int 196: 34–77
Caron L et al. (2017) Geophys J Int 209: 1126-1147
Crawford O et al. (2018) Geophys J Int 214: 1324–1363
Dendy J et al. (2017) Quat Sci Rev 171: 234-244
Dutton A, Lambeck K (2012) Science 337 : 216-219
Kopp RE et al. (2009) Nature 462: 863-867
Kopp RE et al. (2014) Earth’s Future 2: 287–306
Love R et al. (2016) Earth’s Future 4: 440-464
Raymo ME et al. (2011) Nat Geosci 4: 328-332
Raymo ME, Mitrovica JX (2012) Nature 483: 453-456
Slangen ABA et al. (2014) Clim Change 124: 317-332
Tarasov L et al. (2012) Earth Planet Sci Lett 315-316: 30-40
Whitehouse PL (2018) Earth Surf Dyn 6:401-429