On the importance of centennial variability for ice ages

Ditlevsen P & Crucifix M

>Access contents of this issue

>Download this article as pdf

Past Global Changes Magazine

25(3)

152-153

2017

https://doi.org/10.22498/pages.25.3.152

Peter Ditlevsen1 and Michel Crucifix2

Ice ages are paced by astronomical forcing, but how centennial variability affects their dynamics is still unknown.

A common explanation of ice ages asserts that they result from a chain of responses, which follow and then amplify the effects of the changes in the distribution of incoming solar radiation along the seasons and along latitudes. This is the modern interpretation of the Milankovitch theory. From this perspective, the presence of a 100-ka component dominating the frequency spectrum of proxies for ice ages has often been presented as a puzzle. True, changes in eccentricity modulate the amplitude of precession peaks at a period of about 100 ka, but the spectrum of insolation time series do not contain an amplitude peak at this period. Since the dominant period of response differs from the dominant period of forcing, the feedbacks between components of the climate system must involve some non linearity. It was then observed that the dominance of such non linear feedbacks opens the possibility that ice ages may even arise as a self-sustained cycle. With this possibility in mind, the astronomical forcing is often prudently presented as the "pacemaker" of an internal oscillation rather than a primary "driver".

The SPECMAP days

One of the objectives of the Spectral Mapping Project (SPECMAP) in the 1980s was, precisely, to investigate such dynamics (Imbrie et al. 1992). The methodology consisted of filtering climate records along frequency bands at about 1/20, 1/40 and 1/100 ka^-1 in order to characterize the amplitudes of different climatic variables, and estimate leads and lags across them.

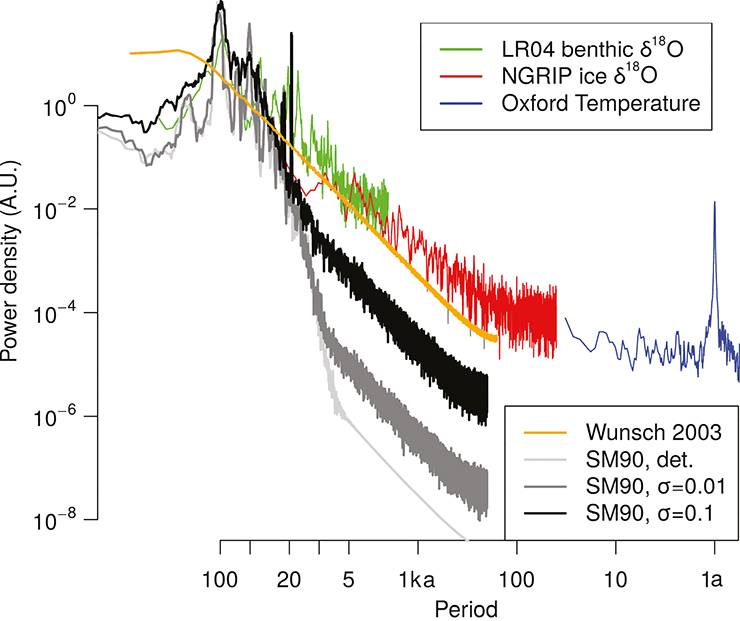
Figure 1: Periodogram of paleoclimatic records: LR04 benthic stack (green), NGRIP isotope record (red), Oxford temperature data adapted from Shao and Ditlevsen (2016; blue), compared to the spectra estimated for the Wunsch (2003) stochastic model (orange), and the Saltzmann Maash 1990 model (thick grey and black, with different levels of added noise; adapted from Crucifix et al. 2016).

In parallel, theorists developed and studied small numerical models expressed in the form of time-difference equations representing interactions between climate components such as ice sheets and the carbon cycle. In such reduced models, the relaxation timescales, which encode the typical response time of system components, are generally of several millennia. Hence, by design, these models do not include variability at millennial frequencies, let alone centennial variability. The idea that justifies only focusing on the representation of the dynamics at a given timescale without caring much about faster dynamics is the hypothesis of timescale separation (Saltzman 1990). This is also what Lovejoy (2017) refers to as the "scale-bound view" in this issue. Unsurprisingly, thus, the power spectrum of the output of such time-difference models shows amplitude peaks at periods of ~20, 40 and 100 ka and essentially no power at shorter or longer periods (Fig. 1, the "SM90 deterministic" model).

A drunkard's walk

Early on, however, several investigators (e.g. Pisias and Moore 1981) remarked that when the power spectrum of climate variations is plotted on a log-log form, the so-called Milankovitch peaks become almost anecdotal. The visual impression is rather that of a noisy process encompassing slow and fast variability. It turns out that, from the point of view of mathematics, it is not very difficult to construct simple stochastic processes having essentially the same power spectrum as that of the paleoclimatic data. The following model was proposed by Wunsch (2003): Imagine that ice volume may randomly increase or decrease, with a statistical preference for increase (because, say, that the average conditions are colder than in the early Pliocene and favor glaciation). In the parlance of dynamical systems theory this is called a random walk with a drift, perhaps better imaged as “a drunkard's walk”. This kind of drifted random walk will unavoidably reach, sooner or later, a threshold which we fix arbitrarily, and at which point we decide that deglaciation occurs.

The two free parameters (drift and threshold) of this model can easily be adjusted to reproduce the broad characteristics of the paleoclimatic deep-ocean sediment record of ice ages. The model spectrum has no scale separation from the high frequencies down to the 100-ka cycle. Milankovitch forcing may then be parsimoniously re-injected either on the drift of the random walk or in a time varying size of the threshold (Huybers and Wunsch 2005).

Two views on ice ages

We thus face two different views on ice ages. In the first view, the modern Milankovitch theory explains ice ages as the result of multiple feedbacks which operate at the timescale of several millennia. Simple deterministic models are the expression of this view and they can be impressively successful at reproducing the broad time evolution of ice age proxies all over the Pleistocene (e.g. Paillard and Parrenin 2004), but they do not reproduce the bulk of the power spectrum. Models in the same vein, or sometimes even more idealized, have been used to study the phenomenon of synchronization of ice ages on the astronomical forcing, or the mid-Pleistocene transition (Ashwin and Ditlevsen 2015).

Figure 2: Accounting for background, sub-millennial variability changes our view of glacial cycles. Shown are trajectories obtained with a conceptual, dynamic-stochastic model of ice ages elaborated by Saltzman and Maasch (1990), in A) its deterministic version, and (B-C) then modified to include a stochastic diffusion process, of amplitude σ (equations and units in Crucifix et al. 2016). Blue, red and black curves correspond to three possible results of the stochastic process, among an infinity of possibilities. With the highest amplitude noise (C), orbital pacing is considerably weakened.

In the second view, stochastic dynamics does capture the spectrum (Wunsch 2003; Fig. 2) but a physical theory on the processes that create these fluctuations, determine their statistical properties, and allow them to accumulate over ice-age timescales, is still lacking. Hence neither view can stand alone in offering a complete explanation of ice ages.

There were some attempts to explain the spectrum with a focus on well-identified, non-linear interactions between climate components. Thirty-five years ago, Le Treut and Ghil (1983) proposed a mechanistic model which represented explicitly some fast (sea-ice) and slow (ice-sheet) processes. The model was chaotic; it generated a broad spectrum, but failed to produce a sequence of events that actually resemble ice ages. Another suggestion is to start from a deterministic model and inject a stochastic process in the equations supposed to represent fast atmospheric fluctuations. The strength of the stochastic process can be tuned to bring the power spectrum closer to that estimated from the equations (Fig. 1, black line). The mathematical object built this way is called a stochastic differential equation. As it turns out, in simple models, the stochastic injection tends to ransack the ice-age cycle to the point of making it quite unstable and broadly unpredictable. The sequence of ice ages becomes also much more random (Fig. 2).

Why centennial variability matters

Of course, research on ice ages is increasingly performed with more sophisticated models. Realistic-looking glacial cycles were recently produced with the Earth system model of intermediate complexity CLIMBER (Ganopolski and Calov 2012). Such a model relies on equations which describe well-identified physical aspects of the ocean, ice sheets, atmosphere and carbon cycle, but lack centennial variability. The model therefore exhibits a form of time separation, which is not verified in the data. On the other hand, general circulation models have been shown to produce almost enough centennial variability, but they do not, yet, reproduce glacial cycles. In fact, we do not know whether attempting to represent the full sequence of glacial cycles is a reasonable target. The presence of centennial variability could make them much more random than we think.

For these reasons, centennial variability must be on the agenda of ice-age experts. The relationship between centennial and astronomical variability is largely uncharted, and yet it could still shape our views on the cause of ice ages.

affiliations

1Niels Bohr Institute, University of Copenhagen, Denmark

2Earth and Life Institute, Université catholique de Louvain, Louvain-la-Neuve, Belgium

contact

Peter Ditlevsen: pditlevnbi.ku.dk