A revised estimate of early Pliocene global mean sea level using geodynamic models of the Patagonian slab window

Authors: Hollyday A, Austermann J, Lloyd A, Hoggard M, Richards F and Rovere A

A new paper published by PALSEA working group members in Geochemistry, Geophysics, Geosystems on "A revised estimate of early Pliocene global mean sea level using geodynamic models of the Patagonian slab window" looks at better understanding the height of global mean sea level during the early Pliocene Epoch.

Specifically, Hollyday, et al pay attention to the shorelines that formed during the early Pliocene Epoch in eastern Patagonia. The authors explain that this era is an important target for sea-level reconstructions because it is home to information on the stability of ice sheets in a climate that is warmer than today. They modelled "both mantle flow and the effects of ice sheet loading changes" and "After subtracting out the effects of solid Earth deformation, we calculate a global mean sea level of 17.5 ± 6.4 m (1σ) in the early Pliocene Epoch." 

With this, the authors conclude that sea level was indeed significantly higher in the early Pliocene Epoch, and can be used to calibrate ice sheet models. 

> Access the article 
> Find out more about the PALSEA working group 

Image:

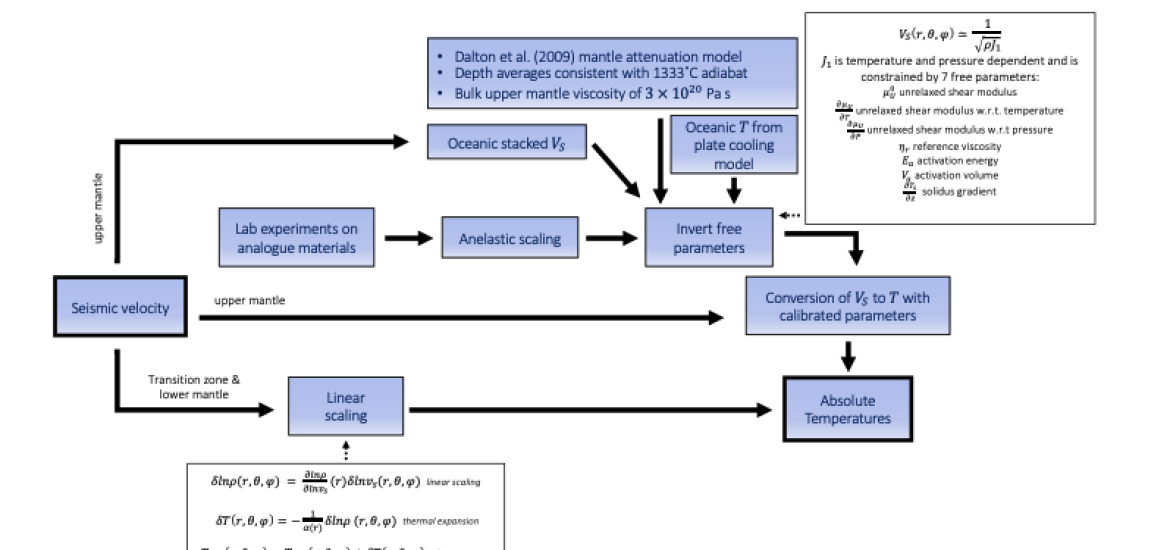
Figure S1.  Workflow of seismic velocity to temperature conversion.  In the lower mantle, we apply a simple linear scaling that converts velocity to density and uses a depth-varying thermal expansivity (Glišović & Forte, 2015) and a reference temperature of 1333˚C.  In the upper mantle, we use a laboratory-based constraint on anelastic deformation of the mantle analogue material, borneol, calibrated with independent geophysical observations of the upper mantle (Yamauchi & Takei, 2016; Richards et al., 2020; see section 3.2 Mantle convection simulations).  This conversion exploits oceanic lithospheric temperatures from a plate cooling model (Richards et al., 2018) in an inverse scheme that identifies seven free parameters (box to the right) from the Yamauchi & Takei (2016) anelastic conversion.  In addition, this inverse parameterization enforces a bulk upper mantle viscosity of 3  1020 Pa s, depth-averaged temperatures consistent with a 1333˚C adiabat, and an attenuation structure in agreement with that of Dalton et al. (2009).  The final parameterization (7 values) is specific to each tomography model.